Bernus, Wilders, Zemlin, Verschelde, Panfilov, 2002
Model Status
This model contains partial differentials and as such can not currently be solved by existing CellML tools.
ValidateCellML detects numerous unit inconsistencies within this model but otherwise verifies it as valid CellML.
Model Structure
Mathematical modelling of cells began over 50 years ago with the work of Hodgkin and Huxley (for the CellML version of the model, see The Hodgkin-Huxley Squid Axon Model, 1952). The first model of cardiac tissue was developed by Noble in 1962 (see Noble Purkinje Fibre Model, 1962), and contained only four variables. During the following years, improvements in both experimental and computational methods lead to the development of successively more accurate models, for example the Luo-Rudy Ventricular Model II (dynamic), 1994, and the Noble Ventricular Cell Model, 1998. Recently, comprehensive models have been published which are cell type specific, for example: Nygren et al., 1998; and Courtemanche et al., 1998 have developed models of atrial cells, while others have produced models of the sinoatrial node: Demir et al., 1999; Zhang et al., 2000; and Boyett et al., 2001, or ventricular myocytes: Puglisi-Bers, 2001 and Pandit et al., 2001.
In 1998, Priebe and Beuckelmann published a model of a single human ventricular cell. This was based mainly on the Luo-Rudy II model for a guinea-pig ventricular myocyte, however, five currents (IKr , IKs , ICa , Ito and IK1 ) were based on experimental data obtained from human myocytes. The remaining currents from the original LR model were scaled to fit human cell data. Priebe and Beuckelmann used their model to compare the electrophysiological properties of healthy and failing ventricular myocytes. The model was accurate, but its complexity and large number of variables make it computationally inefficient. In addition, as a , made up of ordinary differential equations describing the time dependence of membrane potential, gating variables and ion concentrations, the PB model was unstable.
Often it is not necessary to model the ionic currents of a cell with the accuracy and complexity inherent in the biophysically based models. With a view to investigating phenomena on a larger spatial and temporal scale, several ionic current models have been developed that do not seek to model subcellular processes but only to provide an action potential at a minimal computational cost. Such models include The FitzHugh-Nagumo Model, 1961. However, this approach does not reproduce the shape of action potential, which is important in electrocardiography studies. Neither does it allow the analysis of the effects of individual ionic currents on cardiac activation.
In 2002, Bernus et al. published a mathematical model of human ventricular cells, which was somewhere in between the complex PB and the simple FN models. Their new model was simpler, 4.9 times faster, and more stable than the original PB model on which it was based, yet it was sufficiently complex to retain the shape of the action potential at various frequencies, and also the restitution properties of the human ventricular tissue. This was achieved by reducing the original PB model to a six-variable model (see the figure below). Major ionic currents were retained, but some single cell properties that do not have a large influence on the properties of the tissue were discarded. Model simulations were able to reproduce the properties of epicardial, endocardial and M cells by modifying selected ionic currents (this raw CellML model is specific to the epicardial cells). In addition, at the tissue level, Bernus et al. were able to simulate spiral wave behaviour in a 2-D sheet of human ventricular tissue. Simulation results were supported by their agreement with experimental data.
The complete original paper reference is cited below:
A computationally efficient electrophysiological model of human ventricular cells, O. Bernus, R. Wilders, C. W. Zemlin, H. Verschelde, and A. V. Panfilov, 2002, American Journal of Physiology , 282, H2296-H2308. PubMed ID: 12003840
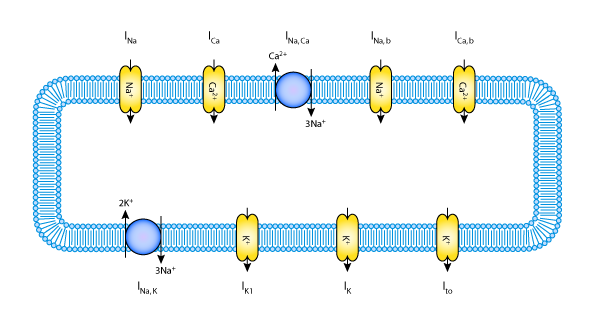 |
| A schematic representation of the ionic currents described by the Bernus et al. 2002 model of a human ventricular cell. The model includes a rapid sodium current, INa; a slow calcium current, ICa; a transient outward current, Ito; a delayed rectifier potassium current, IK; an inward rectifier potassium current, IK1; background sodium and calcium currents, INa,b and ICa,b; a sodium-potassium pump, INaK; and a sodium-calcium exchanger, INaCa. |

