Schneider, Shimayoshi, Amano, Matsuda, 2006
Model Status
This model is known to run in both OpenCell and COR. The current model is based on the M1 model from the paper, but other variants are possible via simple modifications. In particular, to recreate the published results found in most of the paper, Ca(2+) concentration was modeled as an explicit function of time, and graphed on a log scale.
Model Structure
Abstract: A stretch-induced increase of active tension is one of the most important properties of the heart, known as the Frank-Starling law. Although a variation of myofilament Ca(2+) sensitivity with sarcomere length (SL) change was found to be involved, the underlying molecular mechanisms are not fully clarified. Some recent experimental studies indicate that a reduction of the lattice spacing between thin and thick filaments, through the increase of passive tension caused by the sarcomeric protein titin with an increase in SL within the physiological range, promotes formation of force-generating crossbridges (Xbs). However, the mechanism by which the Xb concentration determines the degree of cooperativity for a given SL has so far evaded experimental elucidation. In this simulation study, a novel, rather simple molecular-based cardiac contraction model, appropriate for integration into a ventricular cell model, was designed, being the first model to introduce experimental data on titin-based radial tension to account for the SL-dependent modulation of the interfilament lattice spacing and to include a conformational change of troponin I (TnI). Simulation results for the isometric twitch contraction time course, the length-tension and the force-[Ca(2+)] relationships are comparable to experimental data. A complete potential Frank-Starling mechanism was analyzed by this simulation study. The SL-dependent modulation of the myosin binding rate through titin's passive tension determines the Xb concentration which then alters the degree of positive cooperativity affecting the rate of the TnI conformation change and causing the Hill coefficient to be SL-dependent.
The original paper reference is cited below:
Mechanism of the Frank-Starling law-- A simulation study with a novel cardiac muscle contraction model that includes titin and tropomyosin, Natalie S. Schneider, Takao Shimayoshi, Akira Amano, Tetsuya Matsuda, 2006, Journal of Molecular and Cellular Cardiology, 41, 522-536. PubMed ID: 16860336
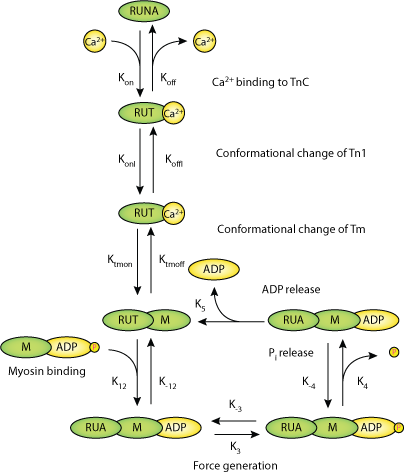 |
| Schematic diagram for the cardiac contraction model (M1). The model consists of seven different states of an RU (RUNA: not activated RU; RUTCaoff: Ca2+ bound to TnC with TnI still bound to A; RUTCaon: TnI released from A; RUTMon: Tm in the activated conformation; RUAMADPPi: M with a hydrolyzed ATP bound to A of a activated RU = weak Xb; M pocket for Pi closed; RUA_MADPPi: strong Xb, M pocket for Pi open; RUA_MADP: strong Xb, Pi released from the acto-myosin complex). Bold rate parameters are dynamic with koffI, ktmon and k3 changing due to cooperativity and k12 depending on titin-based radial force. |

