Lenbury, Ruktamatakul, Amornsamarnkul, 2001
Model Status
Please note that this particular variant of the model is the basic core model which includes three main variables: plasma insulin concentration (x), glucose concentration (y), and the density of the pancreatic beta cells (z) - calculated by equations 11-13. Parameter values have been taken from the legend of figure 2. The model runs in COR and OpenCell and the units are consistent throughout, however the CellML model does not recreate the published results for x (it does for y in figure 2).
Model Structure
ABSTRACT: This paper presents a nonlinear mathematical model of the glucose-insulin feedback system, which has been extended to incorporate the beta-cells' function on maintaining and regulating plasma insulin level in man. Initially, a gastrointestinal absorption term for glucose is utilized to effect the glucose absorption by the intestine and the subsequent release of glucose into the bloodstream, taking place at a given initial rate and falling off exponentially with time. An analysis of the model is carried out by the singular perturbation technique in order to derive boundary conditions on the system parameters which identify, in particular, the existence of limit cycles in our model system consistent with the oscillatory patterns often observed in clinical data. We then utilize a sinusoidal term to incorporate the temporal absorption of glucose in order to study the responses in the patients under ambulatory-fed conditions. A numerical investigation is carried out in this case to construct a bifurcation diagram to identify the ranges of parametric values for which chaotic behavior can be expected, leading to interesting biological interpretations.
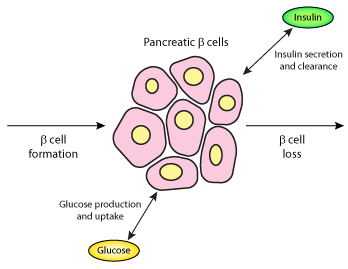 |
| Schematic diagram of the pancreatic beta-cells. Glucose is taken up and produced in response to insulin secretion and clearance. Beta-cell formation and loss represent the rates at which beta-cells replicate and die. |
The original paper reference is cited below:
Modeling insulin kinetics: responses to a single oral glucose administration or ambulatory-fed conditions. Yongwimon Lenbury, Sitipong Ruktamatakul, and Somkid Amornsamarnkul, 2001, Mathematical Biosciences, 59, 15-25. PubMed ID: 11226623

