Spiro, Parkinson, Othmer, 1997
Model Status
This CellML model has been recoded to remove the reaction element. The model runs in both PCEnv and COR but the simulation results may deviate slightly from those which are published in the original paper. We were unsure about the initial conditions used so where we were unsure we set everything to an initial concentration of 0.01 micromolar. Furthermore, where the paper clearly states that Michaelis Menten kinetics were used for the methylation reactions, and Vmax and KR appear in the equations, values for these parameters were not provided. We have derived these values from k1a, k1b and k1c (etc.) but we must highlight that these values may be incorrect. All the units have been checked and are consistent.
Model Structure
In 1997, Peter A. Spiro, John S. Parkinson and Hans G. Othmer published a mathematical model which examined the mechanisms of excitation and adaptation in bacterial chemotaxis (see the figure below). Chemotaxis is the process by which a cell alters its speed or frequency of turning in response to an extracellular chemical stimulus. It is an example of a signal transduction pathway, with features of extreme sensitivity, signal amplification and adaptation: bacteria only respond to changes in their environment rather than to the absolute state of their environment.
In their model, Peter A. Spiro, John S. Parkinson and Hans G. Othmer describe how the phosphorylation cascade and signal amplification account for the extreme bacterial sensitivity to stimuli and how the receptor's multiple methylation states allow adaptation to occur.
The complete original paper reference is cited below:
A model of excitation and adaptation in bacterial chemotaxis, Peter A. Spiro, John S. Parkinson and Hans G. Othmer, 1997, Proc. Natl. Acad. Sci. USA , 94, 7263-7268. (Full text and PDF versions of the article are available to subscribers on the PNAS website.) PubMed ID: 9207079
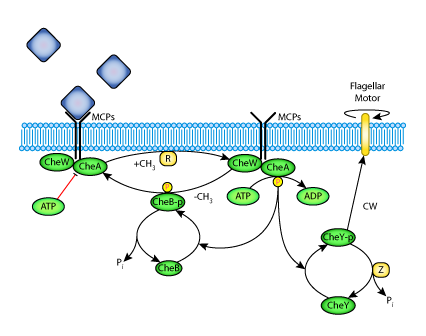 |
| A rendering of a bacterial chemotaxis pathway. |
In CellML, models are thought of as connected networks of discrete components. These components may correspond to physiologically separated regions or chemically distinct objects, or may be useful modelling abstractions. This model has 61 components representing chemically distinct objects (23 chemical species and 38 reactions) and one component defined for modelling convenience which stores the universal variable time. Because this model has so many components, its CellML rendering would be complex. For an example of a CellML rendering of a reaction pathway see The Bhalla Iyengar EGF Pathway Model, 1999.

