Asthagiri, Lauffenburger, 2001
Model Status
This model has been recoded in CellML without the use of the reaction element. The parameters and differential equations described in the original publication were used. This CellML model is known to read in both COR and PCEnv although currently it is unable to recreate the published results from the original model.
ValidateCellML detects widespread unit inconsistency within this model.
Model Structure
In 2001, Anand Asthagiri and Douglas Lauffenburger published a mathematical model which examined the mechanisms that govern MAPK pathway dynamics (see the figure below). Their model builds upon the MAPK cascade model of Chi-Ying Huang and James Ferrell (1996). This earlier model focused on the steady-state effects of signaling, whereas more recently, it has been discovered that a signal's information content partly resides in its dynamics.
In their model, Anand Asthagiri and Douglas Lauffenburger concentrate on the role of negative feedback mechanisms in the generation of signal adaptation - a term referring to the reset of a signal to prestimulation levels. They assess how different modes of feedback affect the properties of MAPK signalling dynamics.
The complete original paper reference is cited below:
A Computational Study of Feedback Effects on Signal Dynamics in a Mitogen-Activated Protein Kinase (MAPK) Pathway Model, Anand R. Asthagiri and Douglas A. Lauffenburger, 2001, Biotechnol. Prog , 17, 227-239. (Full text and PDF versions are available to subscribers on the ACS Publications website. PubMed ID: 11312698
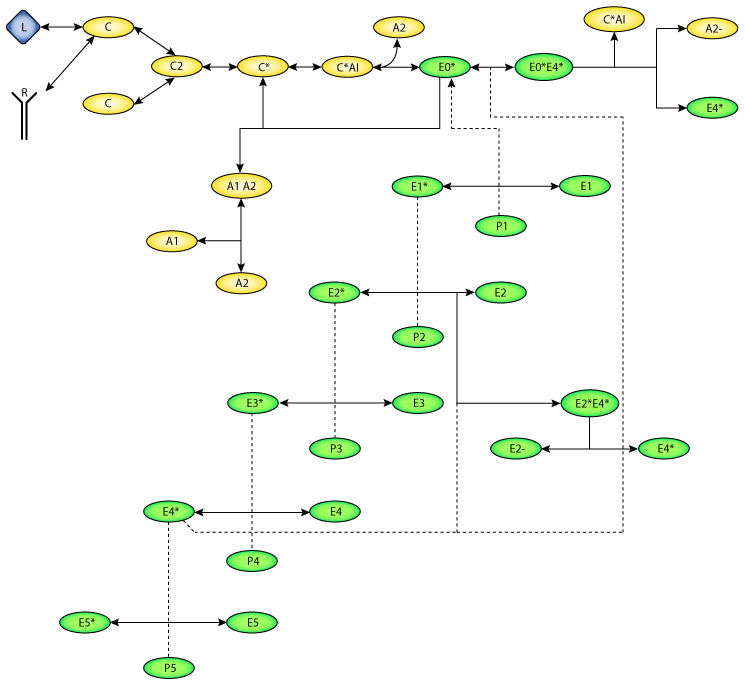 |
| A rendering of the MAPK cascade with feedback effects. Species are represented by rounded rectangles, and reactions by arrows. The action of a catalyst on a reaction is represented by dashed lines. |
In CellML, models are thought of as connected networks of discrete components. These components may correspond to physiologically separated regions or chemically distinct objects, or may be useful modelling abstractions. This model has 71 components representing chemically distinct objects (41 chemical species and 30 reactions) and one component defined for modelling convenience which stores the universal variable time. Because this model has so many components, its CellML rendering would be complex. For an example of a CellML rendering of a reaction pathway see The Bhalla Iyengar EGF Pathway Model, 1999.

